题目相关

题目链接: 洛谷 P1995 程序自动分析

题目描述

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设 $x_1,x_2,x_3,\cdots$ 代表程序中出现的变量，给定 $n$ 个形如 $x_i=x_j$ 或 $x_i\neq x_j$ 的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：$x_1=x_2,x_2=x_3,x_3=x_4,x_4\neq x_1$，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入格式

输入的第一行包含一个正整数 $t$，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第一行包含一个正整数 $n$，表示该问题中需要被满足的约束条件个数。接下来 $n$ 行，每行包括三个整数 $i,j,e$，描述一个相等/不等的约束条件，相邻整数之间用单个空格隔开。若 $e=1$，则该约束条件为 $x_i=x_j$。若$e=0$，则该约束条件为 $x_i\neq x_j$。

输出格式

输出包括 $t$ 行。

输出文件的第 $k$ 行输出一个字符串 YES 或者 NO（字母全部大写），YES 表示输入中的第 $k$ 个问题判定为可以被满足，NO 表示不可被满足。

输入输出样例 #1

输入 #1

1
2
3
4
5
6
7
2
2
1 2 1
1 2 0
2
1 2 1
2 1 1

输出 #1

1
2
NO
YES

输入输出样例 #2

输入 #2

1
2
3
4
5
6
7
8
9
10
2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0

输出 #2

1
2
YES
NO

说明/提示

【样例解释1】

在第一个问题中，约束条件为：$x_1=x_2,x_1\neq x_2$。这两个约束条件互相矛盾，因此不可被同时满足。

在第二个问题中，约束条件为：$x_1=x_2,x_1 = x_2$。这两个约束条件是等价的，可以被同时满足。

【样例说明2】

在第一个问题中，约束条件有三个：$x_1=x_2,x_2= x_3,x_3=x_1$。只需赋值使得 $x_1=x_2=x_3$，即可同时满足所有的约束条件。

在第二个问题中，约束条件有四个：$x_1=x_2,x_2= x_3,x_3=x_4,x_4\neq x_1$。由前三个约束条件可以推出 $x_1=x_2=x_3=x_4$，然而最后一个约束条件却要求 $x_1\neq x_4$，因此不可被满足。

【数据范围】

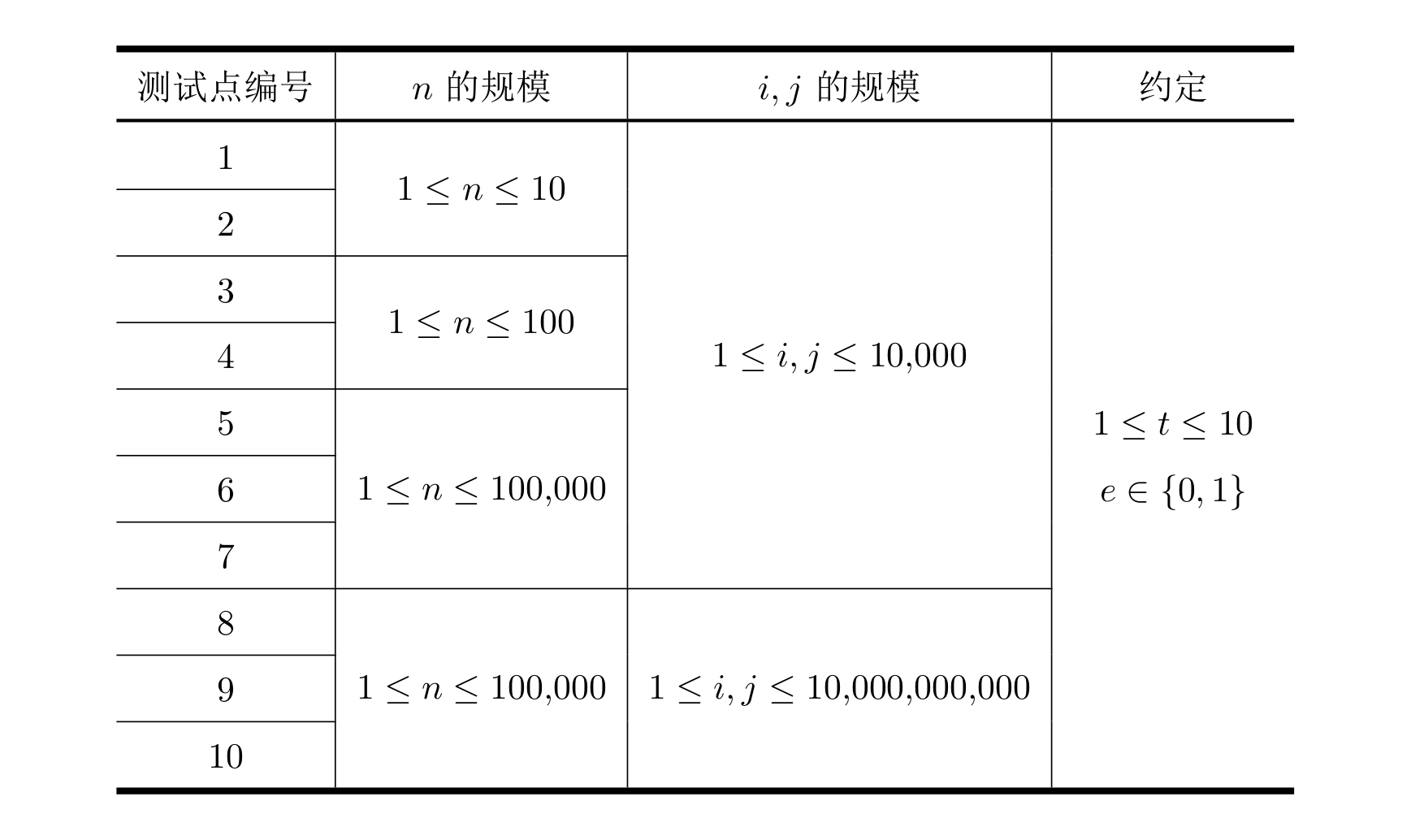
所有测试数据的范围和特点如下表所示：

勘误：测试点 $8 \sim 10$ 的 $i, j$ 约束为 $1 \leq i, j \leq 10^9$，而不是下图中的 $10^{10}$。

题目解析

对于约束相同的 $x$，那么其中的所有元素都必须相同，那么我们可以先处理所有相同的约定，得到所有相同值的元素为一组。

那么再考虑不相同的约束，如果两者在先前计算同一组内，则无法满足条件。

以上的合并与查询可以用并查集解决。

注意到 $i,j$ 的规模较大，但实际输入 $n=10^5$，也即最多有 $2\times10^5$ 个不同的变量。进行离散化处理即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;

struct node {
    int x, y;
    int r;
} a[100010];

int n, t, c[200210], tot, fa[200210];
int unique_num_count;
bool yes;

int find_fa(int x){
    if (fa[x] != x) 
        fa[x] = find_fa(fa[x]);
    return fa[x];
}

int main(){
    scanf("%d", &t);
    while (t--) {
        yes = true;
        scanf("%d", &n);
        tot = 0;
        memset(c, 0, sizeof(c));
        for (int i = 1; i <= 2 * n; ++i) fa[i] = i;
        for (int i = 1; i <= n; ++i) {
            scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].r);
            c[++tot] = a[i].x;
            c[++tot] = a[i].y;
        }
        sort(c + 1, c + 1 + tot);
        unique_num_count = unique(c + 1, c + 1 + tot) - c - 1;
        for (int i = 1; i <= n; ++i) {
            a[i].x = upper_bound(c + 1, c + 1 + unique_num_count, a[i].x) - c - 1;
            a[i].y = upper_bound(c + 1, c + 1 + unique_num_count, a[i].y) - c - 1;
        }
        for (int i = 1; i <= n; ++i) {
            if (a[i].r) {
                int f1 = find_fa(a[i].x), f2 = find_fa(a[i].y);
                if (f1 != f2) 
                    fa[f1] = f2;
            }
        }
        for (int i = 1; i <= n; ++i) {
            if (!a[i].r){
                int f1 = find_fa(a[i].x), f2 = find_fa(a[i].y);
                if (f1 == f2) {
                    yes = false;
                    break;
                }
            }
        }
        if (yes) printf("YES\n");
        else printf("NO\n");
    }
    return 0;
}